Part Two of Upfront vs. Investing

Back on Track

Hello again! Before we get started, while I’m hoping this is evident by the title, in case this post gets way more publicity than the first, I need to let you know that this is Part 2 of a series of posts. If you haven’t read the first, you need to go back and read it, then come back here when you’re done.

3 Click any of these words to get to the first post.

Anyways, let’s get into it!

Incredibly Captivating Cliffhanger

So, where did we leave off? That’s right, with a beautiful picture of a sunset. But that’s not really relevant to the main plot.

More on-topic, I explained to you what Simple and Compound interest are, and how they work. I was then going to explain why those are both not complicated enough to describe what happens to interest on a loan. But then I got distracted, so here we are, a few days later and smarter – hopefully.

Let’s do this.

Interest On A Decreasing Principal

4

The crux

5 of the issue is what I outlined before, where you keep paying interest on whatever is left.
But “whatever is left” is a constantly changing number, and how do you calculate interest on that?
Is there a difference between splitting up your payments into weekly, monthly, and yearly?
When is interest calculated on the loan?
Why do I feel horribly unqualified?
All of these are questions I hope to answer in this article. Except maybe for the last one. That one should be obvious, seeing as you’re reading this on a comic site.

One more challenge I need to mention is that people like regularity, and they would revolt if loans were structured like my example in Part 1, where the theoretical person kept paying more on their loan. People want payments that are the same every month, that they can work into their budget.

Now, it sounds really complicated to first figure out the interest, and then sort of work backwards to figure out how much you’d owe every month. When I first thought of this, I thought you’d have to re-calculate the interest every time someone paid, or something crazy like that. The reality is actually a bit simpler, with a fancy equation that neatly solves the issue for us.

Additionally, what ends up happening in real loans is that the payment is first used to pay off the interest accrued that month, and then the leftovers are used to pay off the balance.

Now we need to figure out how that works. Let’s dig in to some algebra!

The Magic Equation

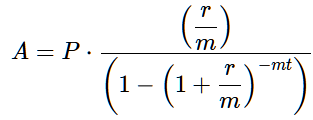
That’s it. And yes, it looks intimidating, with a lot of parentheses and funny letters. I’ll bet it’s even scarier if the last time you found X was on a treasure map.

But don’t worry. I gotchu.

Break it Down

We’ll start by simply explaining what every letter means.

‘A’ is the amount owed every month. That will be our magic answer.
‘P’ is the original amount of the loan, aka the total before interest, aka the principal.
‘r’

8 is the annual interest, in decimal form. For example, 5% would be 0.05.
‘m’

9 is the amount of times interest is calculated on the loan, per year, also known as the compounding period. For example, if interest is added every month, the number would be 12.
‘t’ is the length of the loan, in years.

Take a Deep Breath

Let me stop here and address some questions I think will be popping up around now.

Is this actually relevant? Just tell me how much money I’ll save or lose, and let me go.

Yes, I’ll tie it all together. Just wait and see. If I just told you an answer, you wouldn’t really know what the answer was, you’d just accept it as truth. Which is exactly what I’m trying to change about interest and the black magic behind it.

We have calculators, why are we doing this?

Because in order to understand if we’re saving or losing money, we need to understand where the money is going. It’s easy to punch a number in a calculator, but if you don’t know what you’re doing with the calculator, it’s about as useful as a brick.

Why does this exist? Just give me a simple multiplication problem.

Essentially, it’s because whoever is giving you a loan could have put that money into a savings account and earned interest on it. You are simply paying them back for that lost potential value.

We’re still trying to figure out if financing and investing your money is worth it?

Yes. We’re working on it.

Why can’t you just figure out the math from the leftover money?

Because the “leftover money” will get smaller every month. We need to figure out if investing it will out-earn the interest, even after pulling a payment from it every month.

Can you get back to the math? I’m dying to hear the answer.

How did you get in here, Jason Fenske?!

Okey Dokey, Carry On

Let’s fill in the equation above with our $100k, 5 year loan, and see if it lines up. While we do. I’ll try to explain what each section is doing.

We’ll start by replacing all the variables

10 with the terms of our loan:
P = $100,000 loan total.
r = 5% interest, or 0.05.
m = Times the interest compounds per year, which in our case is 12, or once per month.
t = Years the loan runs for, which is 5 years by us.

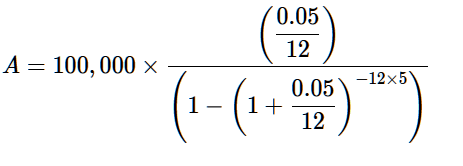
Now, in algebra we love to do a thing called simplify, which is solving the equation piece by piece, tackling it and making it seem a lot less intimidating. In our case, we’ll start with both of the 0.05 ÷ 12 problems, which equal 0.0041667.

This isn’t just a random number, though – this fraction is our monthly interest. It helps if you do it in reverse: If 0.41667% interest was added every month, multiply that by 12 months to get… 5% interest per year!

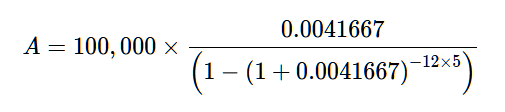
Next comes the 1 + 0.0041667, and the 12 x 5. Adding the one to our monthly interest rate results in a number that can be used to figure out the total balance including interest. For example, 100 x 0.05 is 5, the interest on its own, while 1 x 1.05 is 105, the total plus the interest.

The 12 x 5 is simply making it so we’re working with the total amount of interest periods, which is 12 months x 5 years = 60 in total.

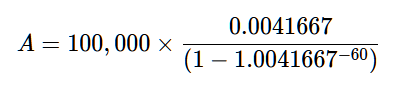
We almost got rid of all the parentheses! Now, this might be a bit confusing, but the little -60 is not “minus sixty”, it’s a negative number. If it was positive, we would get positive interest, as in a savings account. But here, where the money we owe interest on gets less and less, we want the interest to be a negative.

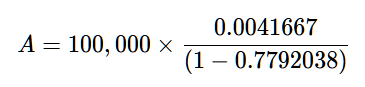
11 That means, the next step is to do 1.0041667 to the power of negative 60. This is essentially ‘all the money we owe including interest’ multiplied by ‘the length of time we owe interest for’. Anyways, it works out to a really long number, but we’re going to stick with the first seven decimal points

12, for a total of 0.7792038.

Almost there! Just a bit of subtraction, which is simply to make sure we’re not dividing by zero.

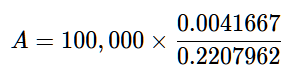
Now we do that division problem, which is how you apply the interest rate to the entire sum of money, including the interest gained.

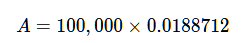
Final step! Multiply our “monthly payment accounting for interest” to our total loan sum…

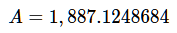
And that’s it! Do you recognize that number? No?

What if you multiply it by 60 months?

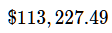
It’s almost exactly the total we found in the previous post, when I used a calculator to get the total of a 5% interest on a $100,000 loan!

The reason why it’s 9¢ off is because we shortened our numbers to 7 decimal places. If you go back and don’t delete any numbers, you’ll get exactly $113,227.40.

Whoop-de-doo

We did it! Next time you look at an insurance calculator, hopefully the black magic looks a little more like a party trick, and less like, you know, real magic.

I want to explain one more point, which is what I mentioned before about how your payment first pays off the interest, and then the leftover goes towards the balance. This is how it works:

The loan of $100,000 increases by 0.41667% every month. So the first month, it’s gained $416.67 in interest, right?
Your first payment of $1,887.12 covers that, plus $1,470.45 of the main balance. So now the balance is $98,529.55.
The next month, it gains another 0.41667% on that new balance, which is an additional $410.54 – less interest than last time, because the balance is less.
You pay another $1,887.12, which, in addition to paying off the interest, lowers the balance by $1,476.58.
And so on, and so forth. Until you’re debt free. Or bankrupt.

Where Were We Again?

But all this was just a very long tangent on our way to our main point, which I will summarize here:

If you had $113,227.40 in a savings account, and you pulled the monthly payments out of that account, would the interest on the savings account be enough to make up for the extra interest you’re paying?

Put another way, if you had $100,000 in that account, would it make enough interest in the five years that you wouldn’t need to add any money to cover the interest on the loan?

That will be answered, in due time. Otherwise known as Part 3!

Thanks for sticking with me, and I’ll see you there!

Head on over to part three by tapping on that “Next Post” at the bottom, or by clicking right here.

If you liked this, and you’re interested in more, why not sign up for our email list? I will only send an email when there’s something new to read, I promise.

If you’re the special kind of monster that read this entire post without reading the previous one, get back there right now and read it, so at least you can get context after the fact.

And finally, leave a comment below on how your brain is holding up so far!